OpenAI Pendulum-v0

pendulum-v0

Observation

• Type: Box(3)

Num	Observation	Min	Max
0	cos(theta)	-1.0	1.0
1	sin(theta)	-1.0	1.0
2	theta dot	-8.0	8.0

Actions

• Type: Box(1)

Num	Action	Min	Max
0	Joint effort	-2.0	2.0

Reward

The precise equation for reward:

-(theta^2 + 0.1theta_dt^2 + 0.001action^2)

Theta is normalized between -pi and pi. Therefore, the lowest cost is -(pi^2 + 0.18^2 + 0.0012^2) = -16.2736044, and the highest cost is 0. In essence, the goal is to remain at zero angle (vertical), with the least rotational velocity, and the least effort.

Starting State

Random angle from -pi to pi, and random velocity between -1 and 1

Observation Spaces

Environment Id	Observation Space	Action Space	Reward Range	tStepL	Trials	rThresh
SemiSupervisedPendulumRandom-v0	Box(3,)	Box(1,)	(-inf, inf)	1000	100	None

pendulum.py

import gym
from gym import spaces
from gym.utils import seeding
import numpy as np
from os import path

class PendulumEnv(gym.Env):
    metadata = {
        'render.modes' : ['human', 'rgb_array'],
        'video.frames_per_second' : 30
    }

    def __init__(self):
        self.max_speed=8
        self.max_torque=2.
        self.dt=.05
        self.viewer = None

        high = np.array([1., 1., self.max_speed])
        self.action_space = spaces.Box(low=-self.max_torque, high=self.max_torque, shape=(1,))
        self.observation_space = spaces.Box(low=-high, high=high)

        self.seed()

    def seed(self, seed=None):
        self.np_random, seed = seeding.np_random(seed)
        return [seed]

    def step(self,u):
        th, thdot = self.state # th := theta

        g = 10.
        m = 1.
        l = 1.
        dt = self.dt

        u = np.clip(u, -self.max_torque, self.max_torque)[0]
        self.last_u = u # for rendering
        costs = angle_normalize(th)**2 + .1*thdot**2 + .001*(u**2)

        newthdot = thdot + (-3*g/(2*l) * np.sin(th + np.pi) + 3./(m*l**2)*u) * dt
        newth = th + newthdot*dt
        newthdot = np.clip(newthdot, -self.max_speed, self.max_speed) #pylint: disable=E1111

        self.state = np.array([newth, newthdot])
        return self._get_obs(), -costs, False, {}

    def reset(self):
        high = np.array([np.pi, 1])
        self.state = self.np_random.uniform(low=-high, high=high)
        self.last_u = None
        return self._get_obs()

    def _get_obs(self):
        theta, thetadot = self.state
        return np.array([np.cos(theta), np.sin(theta), thetadot])

    def render(self, mode='human'):

        if self.viewer is None:
            from gym.envs.classic_control import rendering
            self.viewer = rendering.Viewer(500,500)
            self.viewer.set_bounds(-2.2,2.2,-2.2,2.2)
            rod = rendering.make_capsule(1, .2)
            rod.set_color(.8, .3, .3)
            self.pole_transform = rendering.Transform()
            rod.add_attr(self.pole_transform)
            self.viewer.add_geom(rod)
            axle = rendering.make_circle(.05)
            axle.set_color(0,0,0)
            self.viewer.add_geom(axle)
            fname = path.join(path.dirname(__file__), "assets/clockwise.png")
            self.img = rendering.Image(fname, 1., 1.)
            self.imgtrans = rendering.Transform()
            self.img.add_attr(self.imgtrans)

        self.viewer.add_onetime(self.img)
        self.pole_transform.set_rotation(self.state[0] + np.pi/2)
        if self.last_u:
            self.imgtrans.scale = (-self.last_u/2, np.abs(self.last_u)/2)

        return self.viewer.render(return_rgb_array = mode=='rgb_array')

    def close(self):
        if self.viewer: self.viewer.close()

def angle_normalize(x):
    return (((x+np.pi) % (2*np.pi)) - np.pi)

Pendulum-Motion

Pendulum-Motion

The Sinusoidal Nature of Pendulum Motion

let’s suppose that we could measure the amount that the pendulum bob is displaced to the left or to the right of its equilibrium

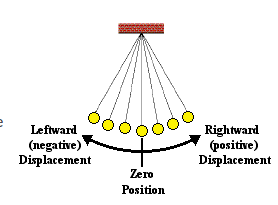
Displacement to the left is regarded as a negative displacement, displacement to the right is as positive displacement. the position of the pendulum bob(measured along the arc relative to its rest position)is a function of the sine of the time.

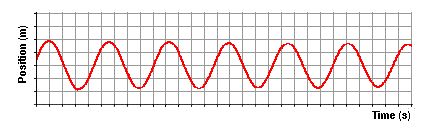
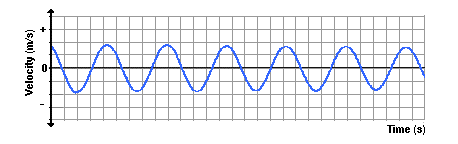
Now let’s see how the velocity of the pendulum changes with respect to the time. As the pendulum bob does the back and forth, the velocity is continuously changing.

• a positive value(for moving rightward)
• a negative value(for moving leftward)

The relationship between the position of the pendulum along the arc of its motion and the velocity with which it moves.

• Position D is zero position
• Position E,F,G are negative positions

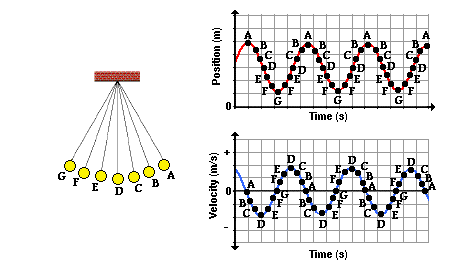
A picture is worth a thousand words.

• The plot above is based upon the equilibrium position(D) being designated as the zero position
• The velocity is least when the displacement is greastest
• The velocity is greatest when the displacement is least
• The further the pendulum has moved away from the equilibrium position,the slower it moves
• The closer the pendulum is to the equilibrium position,the faster it moves

Pendulum equation