Reinforcement Learning Hvass Tutorial Q-Learning
Reinforcement Learning Q-Learning(Off-policy Function Approximation)
Introduction
- Atari games
- Agent just learns how to play it from trial and error
- Input is the screen output of the game and whether the previous action resulted in a reward or penalty
- Playing Atari with Deep RL paper in Deepmind
- Human-level control through deep reinforcement learning paper
- The basic idea is to have the agent estimate so-called Q-values from the image
- The Q-values tell the agent which action is most likely to lead to the highest cumulative reward in the future
- finding Q-values and storing them for later retrieval using a function approximator
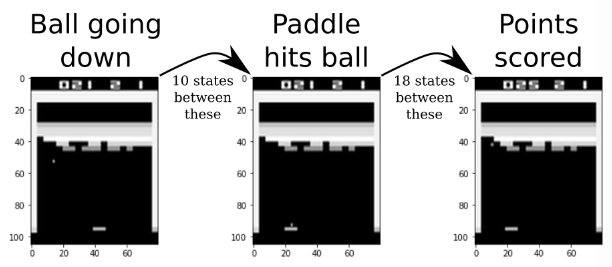
The Problem
- You are controlling the paddle at the bottom
- The goal is maximize the score of smashing the bricks in the wall
- You must avoid dying by letting the ball pass beside the paddle
- Training the states and Q-values below process
Q-Learning
- Q-Learning (Off-policy TD Control)
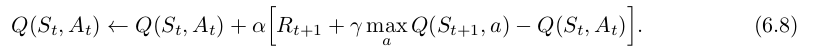in sutton’s book - The Q-values indicate which action is expected to result in the highest reward
- we have to estimate Q-values
- The Q-values are initialized to zero and updated repeatedly as new information is collected from the agent
- Q-value for state and action = reward + discount * max Q-value for next state
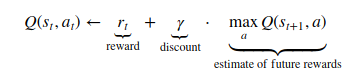
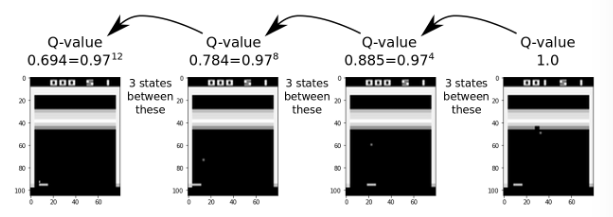
Simple Example
- The images below demonstrates how Q-values are updated in a backwards
- The Agent gets a reward +1 in the right most image
- This reward is then propagated backwards to the previous game-states
- The discounting is an exponentially decreasing function
Detailed Example
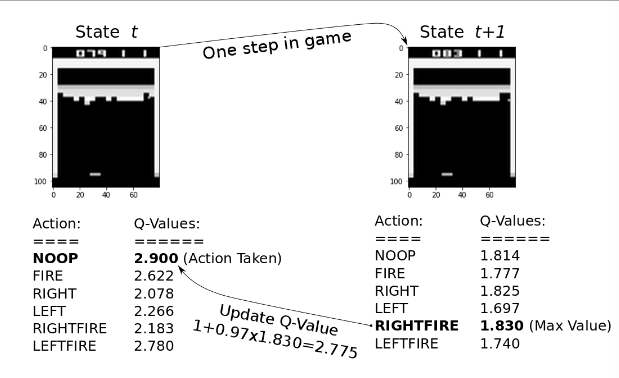
- For the action NOOP in state t is estimated to be 2.9 which is the highest Q-value for that state
- So the agent doesn’t do anything between state t and t+1
- In state t+1, the agent scores 4 points but this is limited to 1 point in this implementation as as to stabilize the training
- The maximum Q-value for state t+1 is 1.83
- we update the Q-value to incorporate this new information
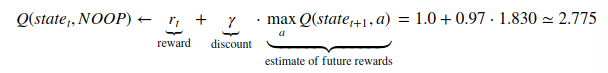
- The new Q-value is 2.775 which is slightly lower than the previous 2.9
- The idea is to have the agent play many,many and update the estimates of the Q-value about reward and penalties
Motion Trace
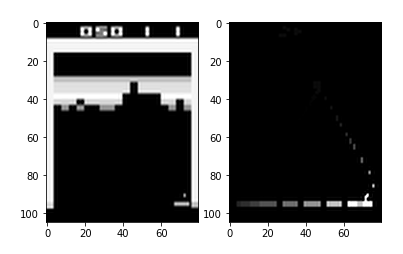
- we can’t know which direction the ball is moving if we just use the single image
- The typical solution is to use multiple consecutive images to represent the state of the game-environment
- We use another approach
- The left image is from the game-environmnet and the right image is the processed image
- The right image shows traces of recent movements
- We can see the ball is going downwards and has bounced off the right wall
- and then the paddle has moved from the left to the right
Training Stability
- consider the 3 images below which show the game-environment in 3 consecutive states
- At state t+1, the score is +1 and it should be 0.97 for state t
- for state t+2, the Neural Network will also estimate a Q-value near 1.0
- It is because the images are so similar
- But this is clearly wrong because the Q-values for state t+2 should be zero as we don’t know anything about future rewards at this point
- For this reason, we will use a so-called Replay Memory so we can get gather a large number of memory of game-state and shuffle them during training the NN
FlowChart
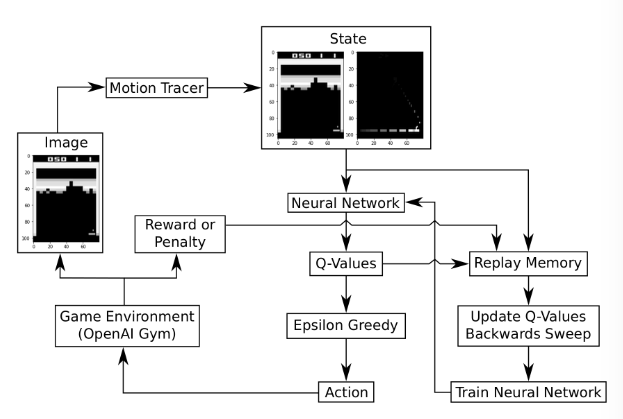
- This flowchart has two main loops
- The first loop is for playing the game and recording data
- NN estimates the Q-values and stores the game-state in the Replay Memory
- The second loop is activated when the Replay Memory is sufficiently full
- First it makes a full backwards propagation
- Then it optimizes NN
Neural Network Architecture
- The NN has 3 convolutional layers, all of which have filter-size 3x3
- The layers have 16,32, and 64 output channels
- The stride is 2 in the first two CNN and 1 in the last layer
- Following the 3 convolutional layers there are 4 fully connected layer each with 1024 units and ReLU activation
Code Analysis
Game Environment
env_name = ‘Breakout-v0’
Download Pre-Trained Model
- You can download a Tensorflow checkpoint which holds all the pre-trained variables for the NN
- 150 hours with 2.6Ghz CPU and GTX 1070 GPU
- The tensorflow checkpoint cann’t be used with newer versions of the gym and atari-py
Hyper parameter
# Description of this program.
desc = "Reinformenct Learning (Q-learning) for Atari Games using TensorFlow."
# Create the argument parser.
parser = argparse.ArgumentParser(description=desc)
# Add arguments to the parser.
parser.add_argument("--env", required=False, default='Breakout-v0',
help="name of the game-environment in OpenAI Gym")
parser.add_argument("--training", required=False,
dest='training', action='store_true',
help="train the agent (otherwise test the agent)")
parser.add_argument("--render", required=False,
dest='render', action='store_true',
help="render game-output to screen")
parser.add_argument("--episodes", required=False, type=int, default=None,
help="number of episodes to run")
parser.add_argument("--dir", required=False, default=checkpoint_base_dir,
help="directory for the checkpoint and log-files")
# Parse the command-line arguments.
args = parser.parse_args()
# Get the arguments.
env_name = args.env
training = args.training
render = args.render
num_episodes = args.episodes
checkpoint_base_dir = args.dir
Create Agent
- The Agent class implements the playing the game, recording data and optimizing the NN
- training = True means replay-memory to record states and Q-values
agent = rl.Agent(env_name=env_name, training=True, render=True, use_logging=False)
model = agent.model
replay_memory = agent.replay_memory
class Agent:
"""
This implements the function for running the game-environment with
an agent that uses Reinforcement Learning. This class also creates
instances of the Replay Memory and Neural Network.
"""
def __init__(self, env_name, training, render=False, use_logging=True):
"""
Create an object-instance. This also creates a new object for the
Replay Memory and the Neural Network.
Replay Memory will only be allocated if training==True.
:param env_name:
Name of the game-environment in OpenAI Gym.
Examples: 'Breakout-v0' and 'SpaceInvaders-v0'
:param training:
Boolean whether to train the agent and Neural Network (True),
or test the agent by playing a number of episodes of the game (False).
:param render:
Boolean whether to render the game-images to screen during testing.
:param use_logging:
Boolean whether to use logging to text-files during training.
"""
# Create the game-environment using OpenAI Gym.
self.env = gym.make(env_name)
# The number of possible actions that the agent may take in every step.
self.num_actions = self.env.action_space.n
- Above codes are :
- create gym.make(env_name)
- get action number from gym environment
# List of string-names for the actions in the game-environment.
self.action_names = self.env.unwrapped.get_action_meanings()
# Epsilon-greedy policy for selecting an action from the Q-values.
# During training the epsilon is decreased linearly over the given
# number of iterations. During testing the fixed epsilon is used.
self.epsilon_greedy = EpsilonGreedy(start_value=1.0,
end_value=0.1,
num_iterations=1e6,
num_actions=self.num_actions,
epsilon_testing=0.01)
- Above codes are:
- create epsilon_greedy policy
- action probability is below than epsilon -> choose random prob
- otherwise use argmax
# With probability epsilon. if np.random.random() < epsilon: # Select a random action. action = np.random.randint(low=0, high=self.num_actions) else: # Otherwise select the action that has the highest Q-value. action = np.argmax(q_values)
if self.training:
# The following control-signals are only used during training.
# The learning-rate for the optimizer decreases linearly.
self.learning_rate_control = LinearControlSignal(start_value=1e-3,
end_value=1e-5,
num_iterations=5e6)
# The loss-limit is used to abort the optimization whenever the
# mean batch-loss falls below this limit.
self.loss_limit_control = LinearControlSignal(start_value=0.1,
end_value=0.015,
num_iterations=5e6)
# The maximum number of epochs to perform during optimization.
# This is increased from 5 to 10 epochs, because it was found for
# the Breakout-game that too many epochs could be harmful early
# in the training, as it might cause over-fitting.
# Later in the training we would occasionally get rare events
# and would therefore have to optimize for more iterations
# because the learning-rate had been decreased.
self.max_epochs_control = LinearControlSignal(start_value=5.0,
end_value=10.0,
num_iterations=5e6)
# The fraction of the replay-memory to be used.
# Early in the training, we want to optimize more frequently
# so the Neural Network is trained faster and the Q-values
# are learned and updated more often. Later in the training,
# we need more samples in the replay-memory to have sufficient
# diversity, otherwise the Neural Network will over-fit.
self.replay_fraction = LinearControlSignal(start_value=0.1,
end_value=1.0,
num_iterations=5e6)
# We only create the replay-memory when we are training the agent,
# because it requires a lot of RAM. The image-frames from the
# game-environment are resized to 105 x 80 pixels gray-scale,
# and each state has 2 channels (one for the recent image-frame
# of the game-environment, and one for the motion-trace).
# Each pixel is 1 byte, so this replay-memory needs more than
# 3 GB RAM (105 x 80 x 2 x 200000 bytes).
# self.replay_memory = ReplayMemory(size=200000,
self.replay_memory = ReplayMemory(size=50000,
num_actions=self.num_actions)
- Above codes are
- Training parameters
- self.learning_rate_control : from 1e-3 to 1e-5
- self.loss_limit_control : from 0.1 to 0.015
- self.max_epochs_control : from 5.0 to 10.0
- self.replay_fraction : from 0.1 to 1.0
- self.replay_memory : RAM size 200000 ~
- Training parameters
# Create the Neural Network used for estimating Q-values.
self.model = NeuralNetwork(num_actions=self.num_actions,
replay_memory=self.replay_memory)
# Log of the rewards obtained in each episode during calls to run()
self.episode_rewards = []
- Above codes are
- create neural network
-
class NeuralNetwork: # Placeholder variable for inputting states into the Neural Network. # A state is a multi-dimensional array holding image-frames from # the game-environment. self.x = tf.placeholder(dtype=tf.float32, shape=[None] + state_shape, name='x') # initial weights init = tf.truncated_normal_initializer(mean=0.0, stddev=2e-2) import prettytensor as pt # Wrap the input to the Neural Network in a PrettyTensor object. x_pretty = pt.wrap(self.x) # Create the convolutional Neural Network using Pretty Tensor. with pt.defaults_scope(activation_fn=tf.nn.relu): self.q_values = x_pretty. \ conv2d(kernel=3, depth=16, stride=2, name='layer_conv1', weights=init). \ conv2d(kernel=3, depth=32, stride=2, name='layer_conv2', weights=init). \ conv2d(kernel=3, depth=64, stride=1, name='layer_conv3', weights=init). \ flatten(). \ fully_connected(size=1024, name='layer_fc1', weights=init). \ fully_connected(size=1024, name='layer_fc2', weights=init). \ fully_connected(size=1024, name='layer_fc3', weights=init). \ fully_connected(size=1024, name='layer_fc4', weights=init). \ fully_connected(size=num_actions, name='layer_fc_out', weights=init, activation_fn=None) # Loss-function which must be optimized. This is the mean-squared # error between the Q-values that are output by the Neural Network # and the target Q-values. self.loss = self.q_values.l2_regression(target=self.q_values_new) self.optimizer = tf.train.RMSPropOptimizer(learning_rate=self.learning_rate).minimize(self.loss) # Used for saving and loading checkpoints. self.saver = tf.train.Saver()
Training
- The agent’s run() is used to play the game
agent.run(num_episodes=2) - run() function
def run(self, num_episodes=None):
"""
Run the game-environment and use the Neural Network to decide
which actions to take in each step through Q-value estimates.
:param num_episodes:
Number of episodes to process in the game-environment.
If None then continue forever. This is useful during training
where you might want to stop the training using Ctrl-C instead.
"""
...
# Counter for the number of states we have processed.
# This is stored in the TensorFlow graph so it can be
# saved and reloaded along with the checkpoint.
count_states = self.model.get_count_states()
-
class NeuralNetwork: self.count_states = tf.Variable(initial_value=0, trainable=False, dtype=tf.int64, name='count_states')
...
while count_episodes <= num_episodes:
if end_episode:
# Reset the game-environment and get the first image-frame.
img = self.env.reset()
# Create a new motion-tracer for processing images from the
# game-environment. Initialize with the first image-frame.
# This resets the motion-tracer so the trace starts again.
# This could also be done if end_life==True.
motion_tracer = MotionTracer(img)
...
- Above codes are
- end_episode = True which cause a reset in the first iteration
- get the first img from gym.env and create class MotionTracer
- Reset the game-environment and Motion Tracer
def _pre_process_image(image): """Pre-process a raw image from the game-environment.""" # Convert image to gray-scale. img = _rgb_to_grayscale(image) # # Resize to the desired size using SciPy for convenience. img = scipy.misc.imresize(img, size=state_img_size, interp='bicubic') return img # class MotionTracer: def __init__(self, image, decay=0.75): """ :param image: First image from the game-environment, used for resetting the motion detector. # :param decay: Parameter for how long the tail should be on the motion-trace. This is a float between 0.0 and 1.0 where higher values means the trace / tail is longer. """ # Pre-process the image and save it for later use. # The input image may be 8-bit integers but internally # we need to use floating-point to avoid image-noise # caused by recurrent rounding-errors. img = _pre_process_image(image=image) self.last_input = img.astype(np.float)
# Get the state of the game-environment from the motion-tracer.
# The state has two images: (1) The last image-frame from the game
# and (2) a motion-trace that shows movement trajectories.
state = motion_tracer.get_state()
# Use the Neural Network to estimate the Q-values for the state.
# Note that the function assumes an array of states and returns
# a 2-dim array of Q-values, but we just have a single state here.
q_values = self.model.get_q_values(states=[state])[0]
- npdstack
class MotionTracer: def get_state(self): # Stack the last input and output images. state = np.dstack([self.last_input, self.last_output]) state = state.astype(np.uint8) return state
# Determine the action that the agent must take in the game-environment.
# The epsilon is just used for printing further below.
action, epsilon = self.epsilon_greedy.get_action(q_values=q_values,
iteration=count_states,
training=self.training)
- class EpsilonGrddy get_action(…)
class EpsilonGreedy: def get_action(self, q_values, iteration, training): epsilon = self.get_epsilon(iteration=iteration, training=training) # # With probability epsilon. if np.random.random() < epsilon: # Select a random action. action = np.random.randint(low=0, high=self.num_actions) else: # Otherwise select the action that has the highest Q-value. action = np.argmax(q_values)
# Take a step in the game-environment using the given action.
# Note that in OpenAI Gym, the step-function actually repeats the
# action between 2 and 4 time-steps for Atari games, with the number
# chosen at random.
img, reward, end_episode, info = self.env.step(action=action)
# Process the image from the game-environment in the motion-tracer.
# This will first be used in the next iteration of the loop.
motion_tracer.process(image=img)
- npwhere
class MotionTracer: def process(self, image): ... img_dif = img - self.last_input img_motion = np.where(np.abs(img_dif) > 20, 255.0, 0.0) ...
# Add the reward for the step to the reward for the entire episode.
reward_episode += reward
# Determine if a life was lost in this step.
num_lives_new = self.get_lives()
end_life = (num_lives_new < num_lives)
num_lives = num_lives_new
# Increase the counter for the number of states that have been processed.
count_states = self.model.increase_count_states()
...
# If we want to train the Neural Network to better estimate Q-values.
if self.training:
# Add the state of the game-environment to the replay-memory.
self.replay_memory.add(state=state,
q_values=q_values,
action=action,
reward=reward,
end_life=end_life,
end_episode=end_episode)
-
class ReplayMemory: # self.num_actions = self.env.action_space.n ... self.states = np.zeros(shape=[size] + state_shape, dtype=np.uint8) self.q_values = np.zeros(shape=[size, num_actions], dtype=np.float) self.actions = np.zeros(shape=size, dtype=np.int) self.rewards = np.zeros(shape=size, dtype=np.float) ...
# How much of the replay-memory should be used.
use_fraction = self.replay_fraction.get_value(iteration=count_states)
# When the replay-memory is sufficiently full.
if self.replay_memory.is_full() \
or self.replay_memory.used_fraction() > use_fraction:
# Update all Q-values in the replay-memory through a backwards-sweep.
self.replay_memory.update_all_q_values()
-
class ReplayMemory: ... def update_all_q_values(self): # Copy old Q-values so we can print their statistics later. # Note that the contents of the arrays are copied. self.q_values_old[:] = self.q_values[:] # num_used is total number of stored states for k in reversed(range(self.num_used-1)): # Get the data for the k'th state in the replay-memory. action = self.actions[k] reward = self.rewards[k] end_life = self.end_life[k] end_episode = self.end_episode[k] # Calculate the Q-value for the action that was taken in this state. if end_life or end_episode: action_value = reward else: action_value = reward + self.discount_factor * np.max(self.q_values[k + 1]) # Error of the Q-value that was estimated using the Neural Network. self.estimation_errors[k] = abs(action_value - self.q_values[k, action]) # Update the Q-value with the better estimate. self.q_values[k, action] = action_value ...
...
# Get the control parameters for optimization of the Neural Network.
# These are changed linearly depending on the state-counter.
learning_rate = self.learning_rate_control.get_value(iteration=count_states)
loss_limit = self.loss_limit_control.get_value(iteration=count_states)
max_epochs = self.max_epochs_control.get_value(iteration=count_states)
# Perform an optimization run on the Neural Network so as to
# improve the estimates for the Q-values.
# This will sample random batches from the replay-memory.
self.model.optimize(learning_rate=learning_rate,
loss_limit=loss_limit,
max_epochs=max_epochs)
-
class NeuralNetwork: def optimize(self, min_epochs=1.0, max_epochs=10, batch_size=128, loss_limit=0.015, learning_rate=1e-3): ... # Prepare the probability distribution for sampling the replay-memory. self.replay_memory.prepare_sampling_prob(batch_size=batch_size) # Number of optimization iterations corresponding to one epoch. iterations_per_epoch = self.replay_memory.num_used / batch_size # Minimum number of iterations to perform. min_iterations = int(iterations_per_epoch * min_epochs) # Maximum number of iterations to perform. max_iterations = int(iterations_per_epoch * max_epochs) # Buffer for storing the loss-values of the most recent batches. loss_history = np.zeros(100, dtype=float) for i in range(max_iterations): # Randomly sample a batch of states and target Q-values # from the replay-memory. These are the Q-values that we # want the Neural Network to be able to estimate. state_batch, q_values_batch = self.replay_memory.random_batch()-
class ReplayMemory: def random_batch(self): ... idx_lo = np.random.choice(self.idx_err_lo, size=self.num_samples_err_lo, replace=False) idx_hi = np.random.choice(self.idx_err_hi, size=self.num_samples_err_hi, replace=False) idx = np.concatenate((idx_lo, idx_hi)) states_batch = self.states[idx] q_values_batch = self.q_values[idx]
# Create a feed-dict for inputting the data to the TensorFlow graph. # Note that the learning-rate is also in this feed-dict. feed_dict = {self.x: state_batch, self.q_values_new: q_values_batch, self.learning_rate: learning_rate} # Perform one optimization step and get the loss-value. loss_val, _ = self.session.run([self.loss, self.optimizer], feed_dict=feed_dict) # Shift the loss-history and assign the new value. # This causes the loss-history to only hold the most recent values. loss_history = np.roll(loss_history, 1) loss_history[0] = loss_val # Calculate the average loss for the previous batches. loss_mean = np.mean(loss_history) # Print status. pct_epoch = i / iterations_per_epoch msg = "\tIteration: {0} ({1:.2f} epoch), Batch loss: {2:.4f}, Mean loss: {3:.4f}" msg = msg.format(i, pct_epoch, loss_val, loss_mean) print_progress(msg) # Stop the optimization if we have performed the required number # of iterations and the loss-value is sufficiently low. if i > min_iterations and loss_mean < loss_limit: break -
# Save a checkpoint of the Neural Network so we can reload it.
self.model.save_checkpoint(count_states)
# Reset the replay-memory. This throws away all the data we have
# just gathered, so we will have to fill the replay-memory again.
self.replay_memory.reset()
if end_episode:
# Add the episode's reward to a list for calculating statistics.
self.episode_rewards.append(reward_episode)
# Mean reward of the last 30 episodes.
if len(self.episode_rewards) == 0:
# The list of rewards is empty.
reward_mean = 0.0
else:
reward_mean = np.mean(self.episode_rewards[-30:])
if self.training and end_episode:
# Log reward to file.
if self.use_logging:
self.log_reward.write(count_episodes=count_episodes,
count_states=count_states,
reward_episode=reward_episode,
reward_mean=reward_mean)
# Print reward to screen.
msg = "{0:4}:{1}\t Epsilon: {2:4.2f}\t Reward: {3:.1f}\t Episode Mean: {4:.1f}"
print(msg.format(count_episodes, count_states, epsilon,
reward_episode, reward_mean))
elif not self.training and (reward != 0.0 or end_life or end_episode):
# Print Q-values and reward to screen.
msg = "{0:4}:{1}\tQ-min: {2:5.3f}\tQ-max: {3:5.3f}\tLives: {4}\tReward: {5:.1f}\tEpisode Mean: {6:.1f}"
print(msg.format(count_episodes, count_states, np.min(q_values),
np.max(q_values), num_lives, reward_episode, reward_mean))
Reference sites
Tutorials
3-B. Layers API (Notebook)
3-C. Keras API (Notebook)
-
Save & Restore (Notebook)
-
Ensemble Learning (Notebook)
-
CIFAR-10 (Notebook)
-
Inception Model (Notebook)
-
Transfer Learning (Notebook)
-
Video Data (Notebook)
-
Fine-Tuning (Notebook)
-
Adversarial Examples (Notebook)
-
Adversarial Noise for MNIST (Notebook)
-
Visual Analysis (Notebook)
13-B. Visual Analysis for MNIST (Notebook)
-
DeepDream (Notebook)
-
Style Transfer (Notebook)
-
Reinforcement Learning (Notebook)
-
Estimator API (Notebook)
-
TFRecords & Dataset API (Notebook)
-
Hyper-Parameter Optimization (Notebook)
-
Natural Language Processing (Notebook)
-
Machine Translation (Notebook)
-
Image Captioning (Notebook)
-
Time-Series Prediction (Notebook)